HP Prime: Diatomic Molecules
 |
| Diatomic Molecules |
The program DIATOMIC will calculate:
* Distance from
the center of mass for each molecule
* Inertia of the
molecule
* Rotational Energy
at level j (j = 0, 1, 2, 3…)
* Vibrational
Energy at level n (n = 0, 1, 2, 3…)
A diatomic molecule is a molecule made of two atoms. Examples are H2, O2,
NaCl (sodium chloride), and CO (carbon monoxide).
Input:
* Mass of the two
molecules, in atomic mass units (u). The
program will convert them to kilograms.
The conversion is 1 u ≈ 1.660538921 * 10^-27 kg
* Distance of the “bar”
between the two molecules. Give this in ångströms, which an ångström is 10^-10 m.
* Rotational and
Vibrational Energy levels. They do not
have to be the same.
* Frequency of the
diatomic molecule in 10^12 Hz.
Typically, molecules and atoms exhibit frequencies in the order of 10^13
Hz.
The formulas are derived from the use of the Schrödinger Equation. While I won’t give much details, a derivation
can be found in many resources, such as this link: http://chemwiki.ucdavis.edu/Physical_Chemistry/Spectroscopy/Rotational_Spectroscopy/Rotational_Spectroscopy_of_Diatomic_Molecules.
This program can be adopted to other graphing
calculators, but here is a version for the HP Prime:
Program DIATOMIC
EXPORT DIATOMIC()
BEGIN
//
EWS 2015-07-09
//
Diatomic Molecule
LOCAL
m1,m2,r,l1,l2,I;
LOCAL
j,n,w;
LOCAL
Er,Ev;
//
Input
INPUT({m1,m2,r,j,n,w},
"Diatomic
Molecule",
{"Mass
1:","Mass 2:",
"r:","J:","N:","freq:"},
{"Mass
in atomic units",
"Mass
in atomic units",
"Distance
in Angstroms",
"Rotational
energy level",
"Vibration
energy level",
"Frequency
(10^12 Hz)"});
//
Integer Parts
n:=IP(n);
j:=IP(j);
//
Convert to kg
m1:=m1*1.660538921ᴇ−27;
m2:=m2*1.660538921ᴇ−27;
//
Convert Angstroms to m;
r:=r/1ᴇ10;
//
Convert to Hz;
w:=w*1ᴇ12;
//
Lengths
l1:=m2*r/(m1+m2);
l2:=m1*r/(m1+m2);
//
Inertia:
I:=m1*l1^2+m2*l2^2;
//
Rotational Energy:
Er:=1.054571726ᴇ−34^2/(2*I)*j*(j+1);
//
Vibrational Energy:
Ev:=(n+1/2)*1.054571726ᴇ−34*w;
//
Results
PRINT();
PRINT("Distance
to Center (m):");
PRINT("From
Mol. 1: "+STRING(l1));
PRINT("From
Mol. 2: "+STRING(l2));
PRINT("Inertia:");
PRINT(STRING(I)+"
kg m^2");
PRINT("Rotational
Energy:");
PRINT(STRING(Er)+"
J");
PRINT("Vibrational
Energy:");
PRINT(STRING(Ev)+"
J");
RETURN({l1,l2,I,Er,Ev});
END;
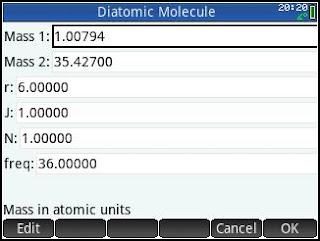
Example
Mass 1:
Hydrogen: 1.00794 u
Mass 2:
Chlorine: 35.4270 u
Distance: 6 ångströms
Frequency: 3.6 x
10^13 Hz
Input Screen:
Output Screen:
Energy:
Rotational: approx.
1.90*10^-23 J
Vibration: approx.
5.69*10^-21 J
Sources:
Strong, Benjamin. “Rotational
Spectroscopy of Diatomic Molecules” http://chemwiki.ucdavis.edu/Physical_Chemistry/Spectroscopy/Rotational_Spectroscopy/Rotational_Spectroscopy_of_Diatomic_Molecules March 26, 2015. Retrieved July 5, 2015.
Wikipedia. “Atom
Vibrations” https://en.wikipedia.org/wiki/Atom_vibrations Retrieved July 9, 2015.
Young, Hugh D. & Roger A Freedman “University Physics with Modern Physics” 11th Ed. Pearson:
San Francisco. 2003
Eddie
This blog is property of Edward Shore. 2015.